기본적인 접근 방식은 분할 정복 알고리즘과 비슷하다. 문제를 부분 문제로 나누어 각 부분 문제의 답을 계산하고, 이 계산한 결괏값을 이용해 원래 문제의 답을 산출한다. 그러나 동적 계획법은 문제를 나눌 때 부분 문제를 최대한 많이 이용하도록 나눈 다음, 주어진 부분 문제의 정답을 한번만 계산하고 저장해둔 뒤 다시 한 번 해당 문제를 풀 때에는 저장해둔 답을 바로 산출하여 속도를 향상한 것이다.
동적 계획벅을 구현하는 방법은 2가지가 있다.
- 하향식으로 문제를 풀어나가는 메모이제이션(Memoization) (주의 :메모라이제이션(Memorization) 아님!!)
- 상향식으로 문제를 풀어나가는 타뷸레이션(Tabulation)
즉, 계산했던 걸 저장한다라는 것이 핵심인 것이다. (캐싱이라고도 불림)
말로 하면 상당히 어려워 보인다. 예시를 통해 보면 쉽게 이해가 갈 것이다.
예시 (피보나치수열 구현하기)
n번째 피보나치 수를 구하는 함수 fib를 구현해보자.
1. 일반적인 재귀 함수를 통해서 구현하기
def fib(n):
if n <= 1:
return n
return fib(n-1)+fib(n-2)2. 메모이제이션(100까지 계산 가능하도록 구현하였다!)
memo = [0]+[1]+[False for _ in range(99)]
def fib(n):
#계산된적 없는 n일 경우 계산해준다.
if not memo[n] and n >= 2:
memo[n] = fib(n-1) + fib(n-2)
return memo[n]
3. 타뷸레이션
memo =[0]+[1]+[False for _ in range(99)]
def fib(n):
#계산된적 없는 n일 경우 계산해준다.
if not memo[n]:
for i in range(2, n+1):
memo[i] = memo[i-1]+memo[i-2]
return memo[n]
이제 이 세 개를 비교해보기 위해 fib(5)를 불렀을 때를 생각해보자.
첫 번째 방법은

해당 그림과 같이 모든 경우의 수를 계산해줘야 하므로 fib함수를 15번 호출해준다.
각 함수들이 얼마나 중복되는지 보면 fib(0) 3번, fib(1) 5번 , fib(2) 3번, fib(3) 2번 중복이 된다.
5라서 직접 셀 수 있는 정도지만 수가 높아지면 셀 수도 없을 만큼 많은 경우의 수가 겹칠 것이다.
시간 복잡도는 O(2^n)으로 n이 많아지면 어마 무시하게 많아진다!!
그에 비해서 메모이제이션과 타뷸레이션으로 구현한 두경우는
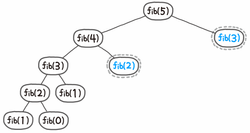
와 같은 경우로 중복되는 경우들이 싹 줄어들었다!
왼쪽의 경우만 새롭게 계산을 해주면 되므로 n개의 경우만 새롭게 계산해주게 된다.
즉, 시간 복잡도는 O(n)이 돼버린 것이다.
동적 계획법을 사용해야 하는 이유에 대해서 알아보았는데
동적 계획법을 구현하는 방법인 메모이제이션과 타뷸레이션을 비교해보도록 하겠다.
메모이제이션(Memoization)
하향식 접근 방법으로 fib(5) -> fib(4) -> fib(3) -> fib(2) -> fib(1)순으로 재귀적으로 불러오게 된다.
- 장점
이렇게 된다면 필요한 계산만 접근 가능하다! - 단점
재귀를 사용하는 만큼 깊이가 깊어지면 과부하에 걸려 오류를 발생시킬 수 있다. - 활용 문제
https://teching.tistory.com/93
백준 9461 : 파도반 수열 (파이썬)
파도반 수열 시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율 1 초 128 MB 58944 25357 20753 41.563% 문제 오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의
teching.tistory.com
타뷸레이션(Tabulation)
하향식 접근 방법으로 fib(2) -> fib(3) -> fib(4) -> fib(5)순으로 반목 문을 통해 구현
- 장점
과부하가 걸릴 위험이 적다. - 단점
하나씩 채워가면서 목푯값까지 계산하므로 필요 없는 계산까지 전부 해주어야 한다. - 활용 문제
https://teching.tistory.com/94
백준 1149 : RGB거리 (파이썬)
RGB거리 시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율 0.5 초 (추가 시간 없음) 128 MB 72867 36485 27248 49.755% 문제 RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번
teching.tistory.com
예시를 피보나치수열로 만들어서 하나의 값을 알려면 모든 경우의 수를 알아야 했기 때문에 필요한 계산만 한다는 말이 무슨 말인가 싶겠지만
https://www.acmicpc.net/problem/9184문제를 풀어보면 둘의 차이를 알 수 있을 것이다!
9184번: 신나는 함수 실행
입력은 세 정수 a, b, c로 이루어져 있으며, 한 줄에 하나씩 주어진다. 입력의 마지막은 -1 -1 -1로 나타내며, 세 정수가 모두 -1인 경우는 입력의 마지막을 제외하면 없다.
www.acmicpc.net
문제의 해설은 https://teching.tistory.com/88
백준 9184 : 신나는 함수 실행
신나는 함수 실행 시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율 1 초 128 MB 20643 8926 6757 42.008% 문제 재귀 호출만 생각하면 신이 난다! 아닌가요? 다음과 같은 재귀함수 w(a, b, c)가 있다. if a
teching.tistory.com
'알고리즘 테스트 > 이론' 카테고리의 다른 글
| 피보나치 수를 구하는 다양한 방법 (2) | 2022.04.06 |
|---|---|
| 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS) (1) | 2022.02.01 |
| 정렬 알고리즘 3 : 계수 정렬(Counting sort) (0) | 2022.01.31 |
| 정렬 알고리즘 2 : 병합 정렬(합병 정렬, Merge sort) (0) | 2022.01.30 |
| 정렬 알고리즘 1 : 버블 정렬 (0) | 2022.01.30 |


