반응형
두 번째로 알아볼 정렬 알고리즘은 바로 병합 정렬이다!
먼저 동작 방식을 간단하게 살펴보자
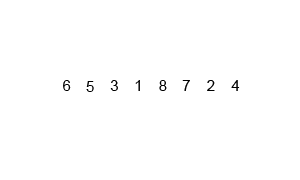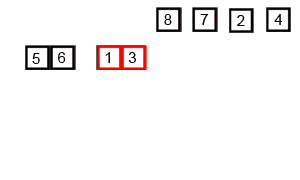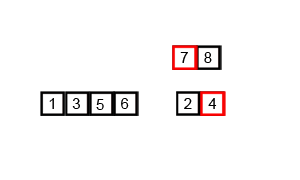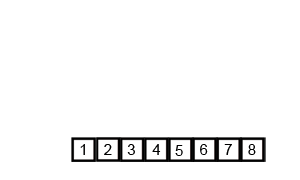
폰 노이만이 개발한 알고리즘으로 데이터 크기만 한 메모리가 더 필요하다는 점이 단점이다.
장점은 데이터의 상태에 영향을 받지 않는다는 점이 있다. 즉, 항상 O(n log(n))의 시간 복잡도를 갖는다.
n-way 합병 정렬이라고 부르지만 나는 흔히 사용하는 2-way 합병 정렬을 알아보도록 하겠다.
- 리스트의 길이가 1이면 이미 정렬된 것으로 본다. (1개밖에 없으므로)
- 정렬되지 않은 리스트를 절반으로 잘라 두 개의 부분 리스트로 나눈다.
- 부분 리스트에 1, 2번 과정을 반복한다.(재귀 이용)
- 잘게 쪼개진 부분리스트 들을 임시 리스트에 합병해가면서 정렬한다.
- 임시 배열에 저장된 결과를 원래 배열에 복사한다.
과정을 그림으로 표현해보면 아래 그림처럼 된다.

참고로 만약 정렬되어있는 두 리스트를 합칠 때 이 방법을 사용하면 가장 빠르게 정렬된 상태로 합칠 수 있다.!
방법을 알아보았으니 구현을 해보자!
구현
파이썬
def mergeSort(nums):
size = len(nums)
if size == 1: return nums
mid = size // 2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
new = [0] * size
end = l = r = 0
while len(left) > l and len(right) > r:
if left[l] > right[r]:
new[end] = right[r]
r += 1
end += 1
else:
new[end] = left[l]
end += 1
l += 1
if len(left) > l: new[end:] = left[l:]
if len(right) > r : new[end:] = right[r:]
return new
nums = [38, 27, 43, 3, 9, 82, 10]
sortedNums = mergeSort(nums)
print(sortedNums)결과

반응형
'알고리즘 테스트 > 이론' 카테고리의 다른 글
| 동적 계획법 (파이썬) (0) | 2022.02.07 |
|---|---|
| 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS) (1) | 2022.02.01 |
| 정렬 알고리즘 3 : 계수 정렬(Counting sort) (0) | 2022.01.31 |
| 정렬 알고리즘 1 : 버블 정렬 (0) | 2022.01.30 |
| 에라토스테네스의 체(소수 판별 알고리즘) (1) | 2021.12.28 |


