반응형
쉬운 계단 수
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
| 1 초 | 256 MB | 96338 | 29894 | 21422 | 29.090% |
문제
45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.
입력
첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
예제 입력 1
1
예제 출력 1
9
예제 입력 2
2
예제 출력 2
17코드
# https://teching.tistory.com/
n = int(input())
cache = {
1: [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]
}
mode = 1_000_000_000
for i in range(2, n + 1):
cache[i] = [0] * 10
for j in range(10):
if j < 9:
cache[i][j] = (cache[i][j]+cache[i - 1][j + 1]) % mode
if j > 0:
cache[i][j] = (cache[i][j]+cache[i - 1][j - 1]) % mode
print(sum(cache[n]) % mode)해설
자릿수를 추가할 때는 뒤에 계단 숫자를 추가하도록 하면 숫자는 무조건 계단수가 된다.
그러므로 숫자를 추가할때 올 수 있는 경우의 수를 확인해주면 된다.
n이 1일 때는 0을 제외한 모든 숫자가 올 수 있다.
n2이 2부터는 맨 뒷자리에 추가할 때
0을 추가할 때는 바로 앞 숫자가 1인 경우에만 붙일 수 있다.
1을 추가할 때는 바로 앞 숫자가 0, 2인 경우에만 붙일 수 있다.
2를 추가할 때는 바로 앞 숫자가 1, 3인 경우에만 붙일 수 있다.
...
9를 추가할 때는 바로 앞 숫자가 8인 경우에만 붙일 수 있다.
그림으로 표현하자면 대충 이러한 모습으로 표현이 된다.
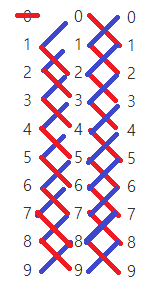
즉, 각 자릿수 별로 맨 마지막 숫자로 올 수 있는 경우의 수들을 저장해주면 된다.
따라서 0을 추가로 붙일 때는 이전 자릿수에서 1을 붙일 때의 경우의 수가 오고
1~8은 i를 붙인다고 생각할 때 이전 자릿수에서 i의 -1 또는 +1을 붙일 때의 경우의 수를 더해주면 된다.
마지막으로 9는 이전 자릿수에서 8을 붙일 때의 경우의 수이다.
해당 알고리즘을 토대로 정리를 해주면 내가 풀이한 코드가 완성된다.
반응형
'알고리즘 테스트 > 백준' 카테고리의 다른 글
| 백준 11053 : 가장 긴 증가하는 부분 수열 (파이썬) (0) | 2022.02.15 |
|---|---|
| 백준 2156 : 포도주 시식 (파이썬) (1) | 2022.02.14 |
| 백준 1463 : 1로 만들기 (파이썬) (0) | 2022.02.12 |
| 백준 2579 : 계단 오르기 (파이썬) (0) | 2022.02.11 |
| 백준 1932 : 정수 삼각형 (파이썬) (1) | 2022.02.10 |

